The term capacitance is the energy storage capacity of capacitors that are positively (+q) or negatively (–q) charged plates. So capacitance is the property of a single capacitor or a set of capacitors measured in Farad (F). The electric field between the plates of a charged capacitor is determined by the charge provided to the capacitor and is directly proportional to the voltage (V) supplied to the capacitor as given by the formula below.

In the formula, C=Q/V the C illustrates the constant of proportionality and is referred as the capacitance of the capacitor. In this article, we will focus on the series and parallel connection of capacitor and their properties as well as their applications in detail.
Series and Parallel Capacitors:
I. Series Combination of Capacitors and Characteristics:
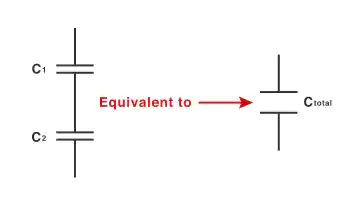
In the case of the series combination of capacitors the series capacitors’ individual capacitances are greater than the total capacitance. In case when two or more than two capacitors are attached in series a single capacitor has the sum of total spaces between the plates of the individual capacitor as its overall effect. All the other factors remain unchanged when we increase the space between the capacitor plates as shown in the diagram below
So as mentioned above the overall capacitance will be less than one as well as will be less than each of the individual capacitors attached in the series connection. The formula to calculate the total capacitance is given below

Current Characteristics in Series Combination:
In the case of current characteristics of the capacitor connected in the series circuit, the DC current cannot pass through the capacitors due to the capacitative blocking effect of the capacitors. However, as per the characteristic study of series circuits, the current flowing through each capacitor is the same. For all series circuits, this is a very common phenomenon and consistent with the series resistor circuit as well. Regardless of the capacitance value the amount of the charge stored in the capacitor is the same as the current flowing through each series capacitor is same.
II. Parallel Combination of Capacitors and Characteristics:
On the other hand, In the case of the parallel combination of capacitors the parallel capacitors’ individual capacitances are equal to the total capacitance. In case when two or more than two capacitors are attached in parallel combination a single capacitor’s capacitance is the total spaces between the plates of individual capacitors as its overall effect. All the other factors remain unchanged when we increase the space between the capacitor plates and hence the results in an increase in capacitance as shown in the diagram below

So as mentioned above the overall capacitance will be more than one as well as will be greater than each of the individual capacitors attached to the series connection. The formula to calculate the total capacitance is given below

As we noticed the properties shown by the capacitors here are exactly the opposite in the case of the series and parallel connection of the resistors.
Current Characteristics in Parallel Combination:
In the case of the parallel combination of capacitors, the AC signal will be able to pass through the capacitors connected in parallel separately. The higher the frequency the larger the amount of AC current will flow keeping the same AC signal conditions through each parallel capacitor. Due to the smaller capacitive reactance and large capacity in a capacitor, the larger capacitor will have a larger current. On the other hand the larger the capacitive reactance and the smaller the capacity in a capacitor, the smaller the capacitor will have a larger current.
The amount of charge stored in each capacitor connected in parallel may vary because, in a parallel capacitor circuit, the current flowing through each capacitor may not be equal however it will be equal in case when the capacitance of the connected capacitor in the circuit is the same. Due to the large charging current in a large-size capacitor, it will have more capacity to store charge. So this ability to store charge is directly proportional to the current flowing through the capacitor.
Applications:
Capacitors play a very important role in the number of applications due to their properties providing good stability and current capabilities. A few of them are discussed below.
· Capacitors can act as energy-storing devices in circuits which is their primary property. When the power is disconnected the capacitors can still consume the energy acting as a temporary battery.
· The capacitors having the property of high voltage functionalities and low inductance, provide missive electric current levels in different types of pulsed power devices.
· Power conditioning can be done by capacitors which is a widely used phenomenon in power supplies.
· Capacitors are used for power factor correction and measured in VA instead of farad in several power supply distributions.
· At tremendous amounts of energy levels, disastrous electric shocks could occur if the massive amount of stored energy isn’t handled correctly. So capacitors having the ability to disengage themselves for a significant time makes them suitable as a safety devices in different electrical systems.
· When we are required to provide the power of supply to a circuit for a short moment the hold-up ability of the capacitor plays a vital role in this regard. The capacitor is more helpful than the small rechargeable batteries used before the development of the capacitor.
· In the phenomenon of coupling and decoupling devices, capacitors can be used in RF.
· In conjunction with power supplies, the decoupling capacitors are referred to by professionals as the smoothing capacitors. While receiving a signal from a rectifier or transformer the waveform is not always smooth and varies between a voltage range of starting point to end point that is zero and peak voltage level respectively. In this case the smoothing or in other words the decoupling is done by the capacitors for DC voltage.